Activation_functions_in_dl

Activation functions

Description

Activation functions works like an on-off button that determines whether the output of a neuron or what information should be passed to next layer. In biology, it works like synaptic in brain which decides what information it passes from one neuron cell to next one. There are several activation functions widely used in neural networks.

Binary function (step function)

In one word, the output of binary function is 1 or 0 which is based on whether the input is greater or lower than a threshold. In math, it looks like this: f(x) = {1, if x > T; 0, otherwise}.

Cons: it does not allow multiple outputs, and it can not support to classify inputs to one of categories.

Linear function

f(x) = $cx$. Cons: 1. the deviation of linear function is a constant, which does not help for backpropagation as the deviation is not correlated to its inputs, in another word, it can not distinguih what weights or parameters help to learn the task; 2. linear function makes the entire multiple neural network into one linear layer (as the combination of linear functions is still a linear function), which becomes a simple regression model. It can not handle complex tasks by varying parameters of inputs.

Non-linear functions

Non-linear functions address the problems by two aspects:

1. The deviation of non-liear function is a function correlated to its inputs, which contributes the backpropagation to learn how to update weights for high accurancy.
2. Non-linear functions form the layers with hidden neurons into a deep neural network which is capable of predicting for complicated tasks by learning from complex datasets.

There are several popular activation functions used in modern deep neural networks.

Sigmoid/Logistic Regression

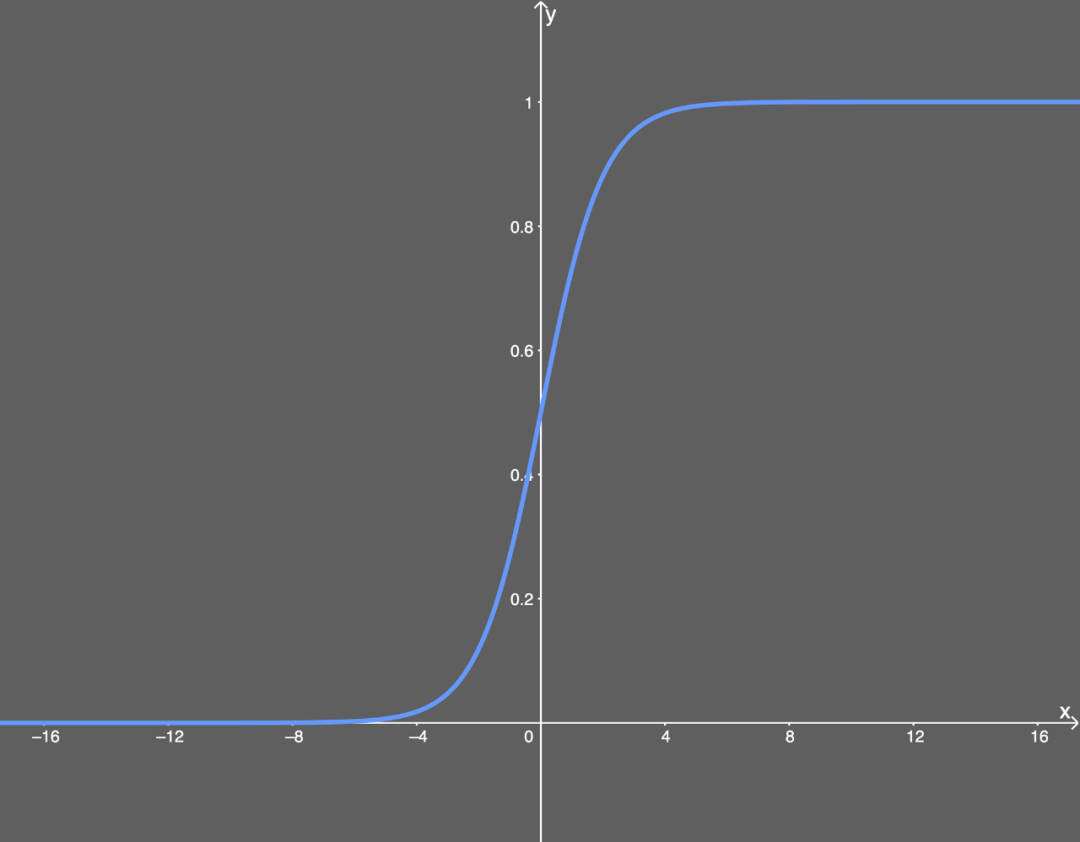
Equation: $$Sigmoid(x) = \frac{1}{1+e^{-x}}$$ Derivative (with respect to $x$): $$Sigmoid^{'}(x) = Sigmoid(x)(1-Sigmoid(x))$$ Pros:

1. smooth gradient, no jumping output values compared to binary function.
2. output value lies between 0 and 1, normalizing output of each neuron.
3. right choice for probability prediction, the probability of anything exists only between 0 and 1.

Cons:

1. vanishing gradient, the gradient barely changes when $x>2$ or $x<-2$.
2. computationally expensive.
3. non zero centered outputs. The outputs after applying sigmoid are always positive, during gradient descent, the gradients on weights in backpropagation will always be positive or negative, which means the gradient updates go too far in different directions, and makes the optimization harder.

Softmax

$$Softmax(x_i)= \frac{x_i}{\Sigma_{j=1}^{n}{x_j}}$$

Pros: capable of handling multiple classification and the sum of predicted probabilities is 1. Cons: only used for output layer.

Softmax is more suitable for multiple classification case when the predicted class must and only be one of categories. k-sigmoid/LR can be used to classify such multi-class problem that the predicted class could be multiple.

Tanh

Equation: $$tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$$ Derivative (with respect to $x$): $$tanh^{'}(x) = 1 -tanh(x)^2$$

Pros:

1. zero centered. make it easier to model inputs that have strongly positive, strongly negative, and natural values.
2. similar to sigmoid

Cons:

1. vanishing gradient
2. computationally expensive as it includes division and exponential operation.

Vanishing gradient

Vanishing gradient means that the values of weights and biases are barely change along with the training.

Exploding gradient

Gradient explosion means that the values of weights and biases are increasing rapidly along with the training.

ReLU

Equation: $$ReLU(x) = max(0, x)$$ Derivative (with respect to $x$): \begin{equation} ReLU^{'}(x) = \begin{cases} 0, &x \leqslant 0; \newline 1, & x > 0 \end{cases} \end{equation} Pros:

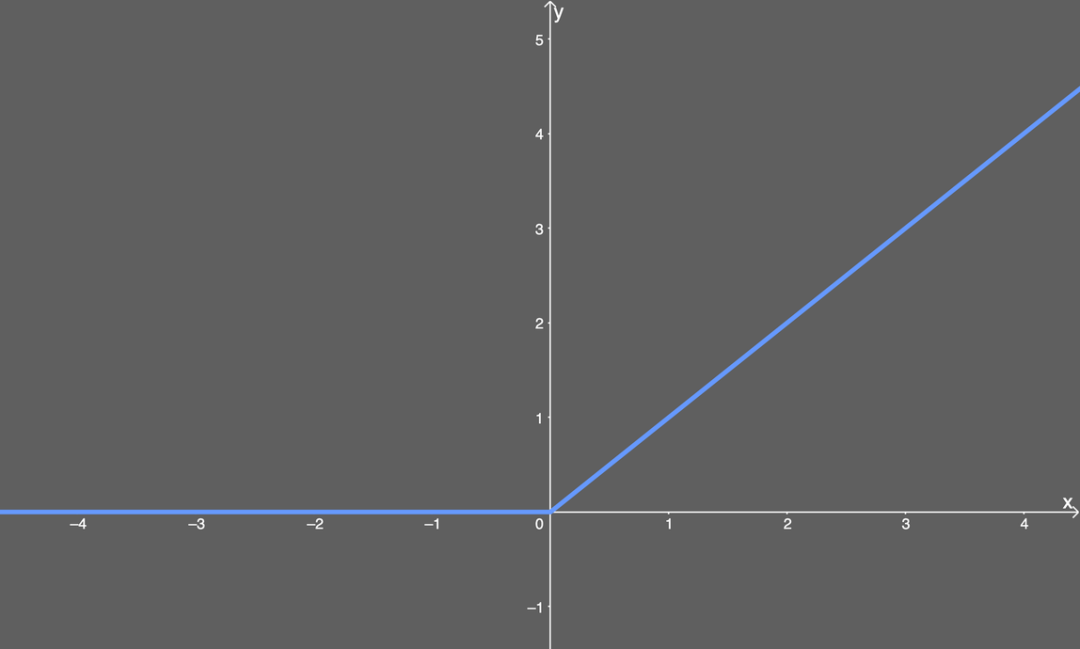
1. computationally efficient
2. non-linear

Why ReLU performs better in modern NNs? The answer is not so sure right now, but its propeties like non-saturation gradient and computionally efficient indeed lead to fast convergence. Additionally, its property sparsing the network also improves the modeling preformance. The non-zero centered issue can be tackled by other regularization techniques like Batch Normalization which produces a stable distribution for ReLU.

Cons:

1. Dying ReLU problem. The backpropagation won’t work when inputs approach zero or negative. However, to some extent, dying ReLU problem makes input values sparse which is helpful for neural network to learn more important values and perform better.
2. Non differentiable at zero.
3. Non zero centered.
4. Don’t avoid gradient explode

ELU

Equation: \begin{equation} ELU(x) = \begin{cases} \alpha (e^x-1), & x \leqslant 0 \newline x, &x > 0
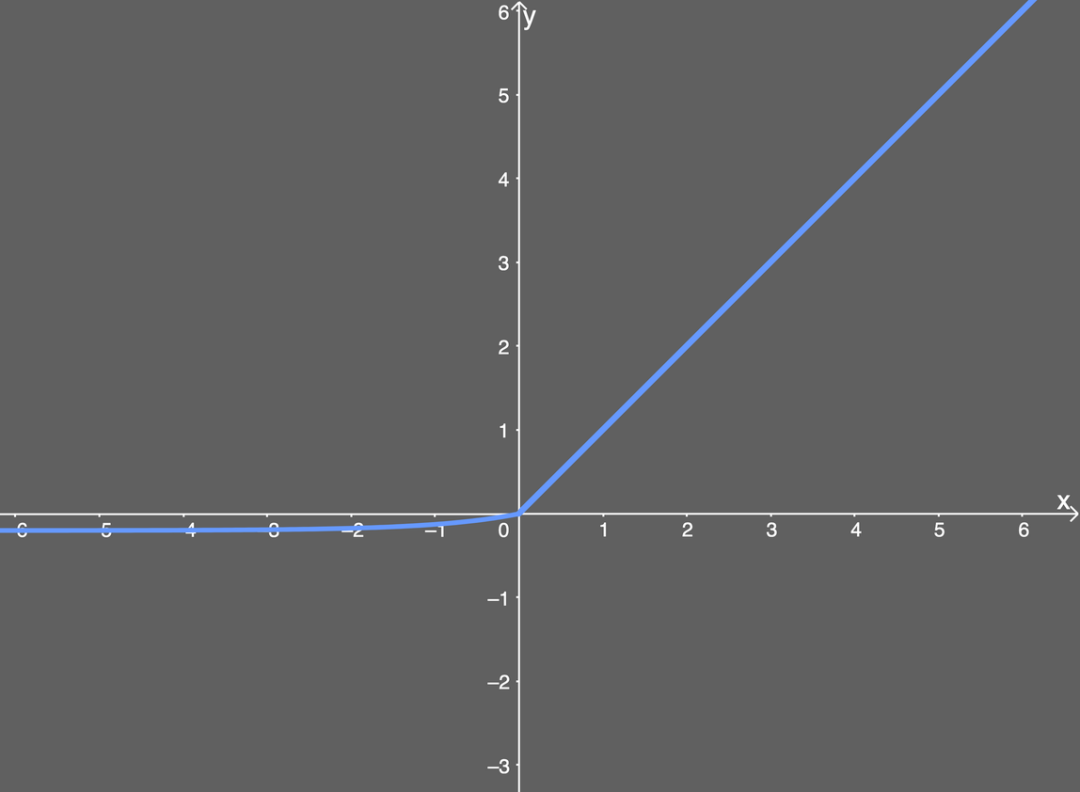
\end{cases} \end{equation}

Derivative: \begin{equation} ELU^{'}(x) = \begin{cases} ELU(x) + \alpha, & x \leqslant 0 \newline 1, & x > 0 \end{cases} \end{equation}

Pros:

1. prevent dying ReLU problem.
2. gradient works when input values are negative.
3. non-linear, gradient is not zero.

Cons:

1. don’t avoid gradient explode.
2. not computationally efficient.
3. $\alpha$ is not learnt by neural networks.

Leaky ReLU

Equation: \begin{equation} LReLU(x) = \begin{cases} \alpha x, &x \leqslant 0 \newline x, &x > 0 \end{cases} \end{equation}

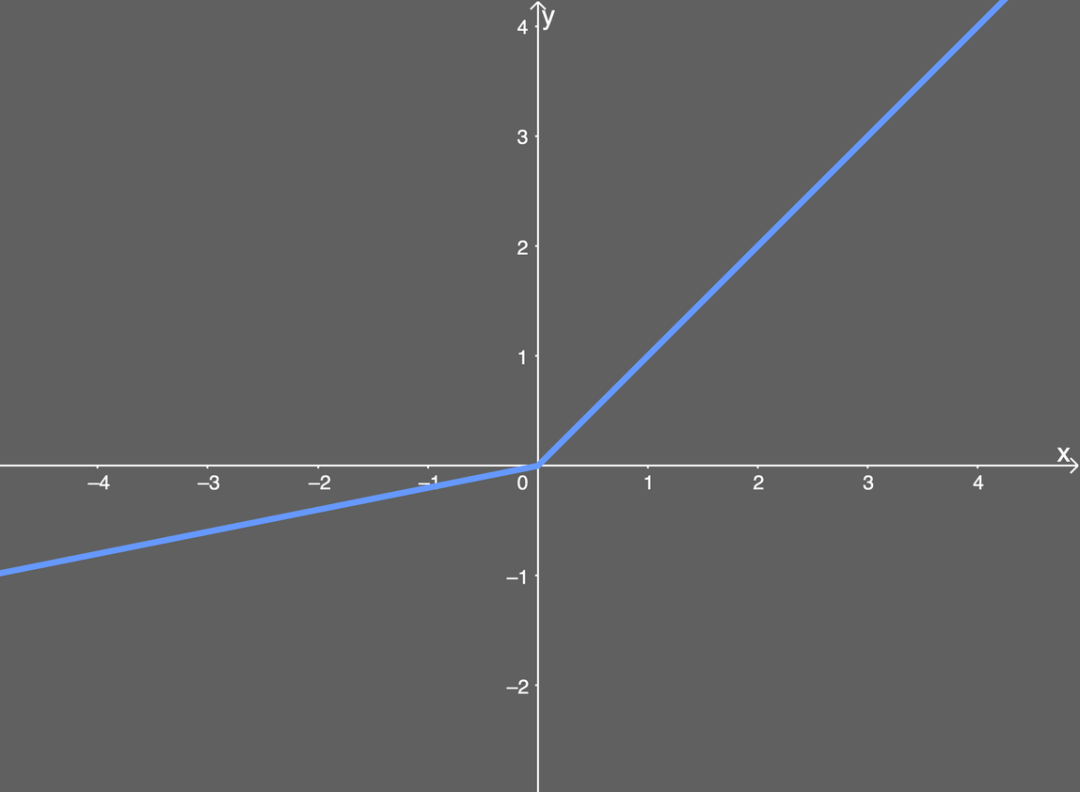
Derviative: \begin{equation} LReLU^{'}(x) = \begin{cases} \alpha, &x \leqslant 0 \newline 1, &x > 0 \end{cases} \end{equation}

Pros:

1. prevent Dying ReLU problem
2. computationally efficient
3. non-linear

Cons:

1. don’t avoid gradient explode
2. Non consistent results for negative input values.
3. non-zero centered
4. non differentiable at Zeros

SELU

Equation: \begin{equation} SELU(x) = \lambda \begin{cases} \alpha e^x-\alpha, & x \leqslant 0 \newline x, & x > 0 \end{cases} \end{equation}

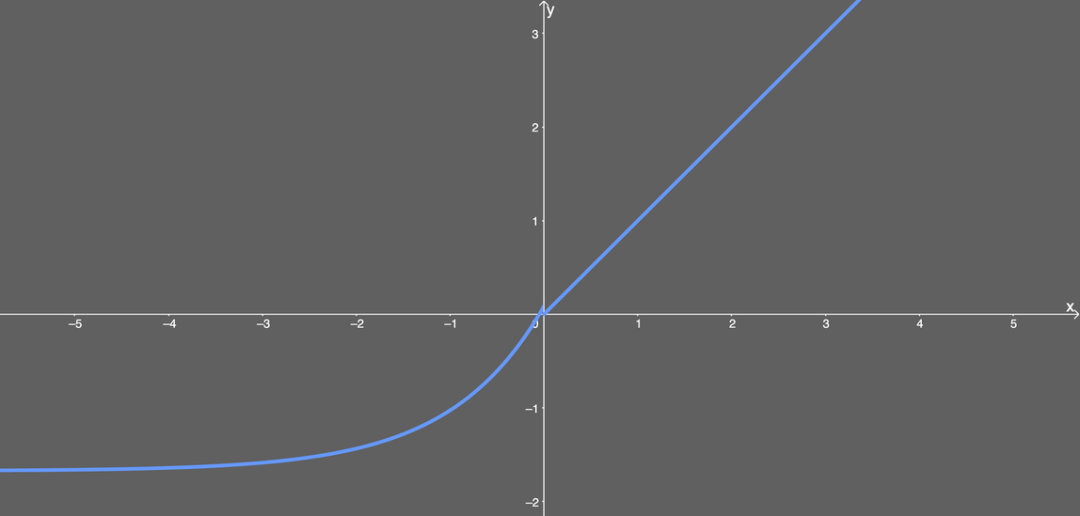
Derivative: \begin{equation} SELU^{'}(x) = \lambda \begin{cases} \alpha e^x, & x \leqslant 0 \newline 1, & x > 0 \end{cases} \end{equation} where $\alpha \approx 1.6732632423543772848170429916717$ and $\lambda \approx 1.0507009873554804934193349852946$.

Pros:

1. Internal normalization, which means faster convergence.
2. Preventing vanishing gradient and exploding gradient.

Cons: Need more applications to prove its performance on CNNs and RNNs.

GELU

Equation: \begin{equation} GELU(x) = 0.5x(1 + tanh(\sqrt{\frac{2}{\pi}} (x + 0.044715x^3))) \end{equation}

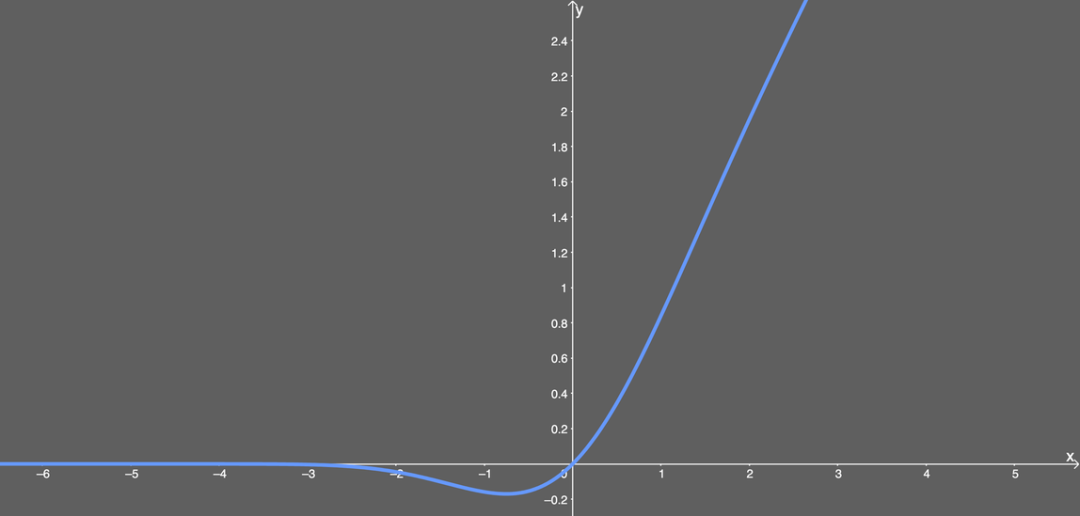
Pros:

1. Best performance in NLP, especially BERT and GPT-2
2. Avoid vanishing gradient

Cons: Need more applications to prove its performance.

Reference

1. https://missinglink.ai/guides/neural-network-concepts/7-types-neural-network-activation-functions-right/
2. https://www.jianshu.com/p/6db999961393
3. https://towardsdatascience.com/activation-functions-b63185778794
4. https://datascience.stackexchange.com/questions/23493/why-relu-is-better-than-the-other-activation-functions