Attention

Attention

The attention mechanism was created to simulate the human visual attention on images or understanding attention on texts. It was firstly born for solving a problem that widely exists in natural language processing (NLP) models like seq2seq, which NLP models often tend to forget the first part of processed sentences.

Seq2seq model

The encoder-decoder architecture commonly used in Seq2seq model:

1. encoder, compress the input sentence into a context vector in a fixed length way which is regarded as a representation of the meaning of input sentence.
2. decoder, fed by the context vector and translate the vector to output. In some early works, the last state of encoder is usually used as the initial state of decoder.

Both of the encoder and decoder are recurrent neural networks, using LSTM or GRU units.

The critical problem of seq2seq model. The seq2seq model often forgets the first part of a long sentence once it completes translation from the entire sentence to a context vector. To address this problem, the attention mechanism is proposed.

The attention mechanism

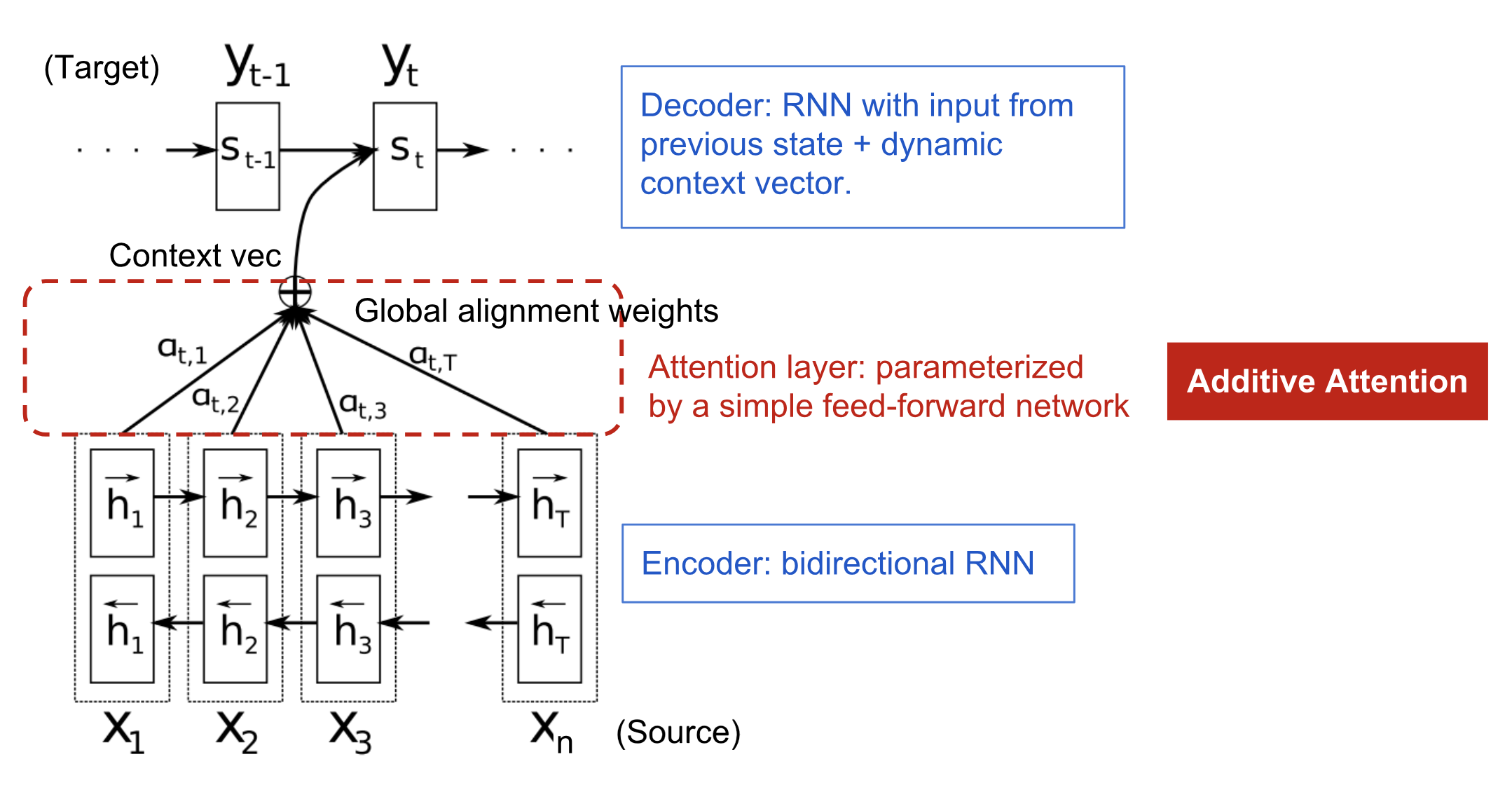
The new architecture for encoder-decoder machine translaion is as following:

The encoder is composed by a bidirection RNN, a context vector is the sum of weighted hidden states and the decoder translates the context vector to a output target based on previous output targets.

Formula

Let x=$(x_1, x_2,…,x_n)$ denote the source sequence of length $n$ and y=$(y_1, y_2,…,y_m)$ denote the output sequence of length $m$, $\overrightarrow{h_i}$ denotes the forward direction state and $\overleftarrow{h_i}$ presents the backward direction state, then the hidden state for $i$th input word is fomulated as: $$h_i = [\overrightarrow{h_i}^T; \overleftarrow{h_i}^T], i=1,2,…,n$$

The hidden states at position $t$ in decoder includes previous hidden states $s_{t-1}$, previous output target $y_{t-1}$ the context vector $c_t$, which is denoted as $s_{t} = f(s_{t-1}, y_{t-1}, c_{t})$, where the context vector $c_{t}$ is a sum of encoder hidden states of input sequence, weighted by alignment scores. For output target at position $t$, we have: $$c_{t} = \sum_{i=1}^{n} \alpha_{t,i} h_i$$

$$ \alpha_{t,i}= align(y_t, x_i) = \frac{exp(score(s_{t-1},h_i))}{\Sigma^n_{i=1} exp(score(s_{t-1},h_{i}))} $$ The score $\alpha_{t,i}$ is assigned to the pair $(y_t, x_i)$ of input at position $i$ and output at position $t$, and the set of weights ${\alpha_{t,i}}$ denotes how much each source hidden state matches for each output. In Bahdanau et al. 2015, the score $\alpha$ is learnt by a feed-forward network with a single hidden layer and this network is jointly learnt with other part of the model. Since the score is modelled in a network which also has weight matrices (i.e., $v_a$ and $W_a$) and activation layer (i.e., tanh), then the learning function is fomulated as: $$score(s_t, h_i) = v_a^T tanh(W_a[s_t;h_i])$$

Self-attention

Self-attention (or intra-attention) is such an attention mechnaism that assigns correlation in a single sequence for an effective representation of the same sequence. It has been shown to be very useful in machine reading, abstractive summarizatin or image description generation.

In Cheng et al., 2016, an application of self-attention mechanism is shown in machine reading. For example, the self-attention mechanism enables the model to learn a correlation between the current word and the previous part of the input sentence.

Soft and Hard Attention

In image caption generation, the attention mechanism is applied and shown to be very helpful. Xu et al.,2015 shows a series of attention visualization to demonstrate how the model learn to summarize the image by paying attention to different regions.

The soft attention and hard attention is telled by whether the attention has access to the entire image or only a patch region:

Soft attention: the alignment weights are assigned to all the patches in the source image, which is the same type used in Bahdanau et al. 2015 Pro: the model is smooth and differentiable Con: computationally expensive when the source image is large

Hard attention: the alignment weights are only assigned to a patch in the source image at a time Pro: less computation at the inference time Con: the model is non-differentiable and requires more complicated techniques such as variance reduction and reinforcement learning to train.(Luong et al., 2015)

why hard attention is non-differentiable? Hard attention is non-differentiable because it’s stochastic. Both hard and soft attention calculate a context vector using a probability distribution (usually over some set of annotation vectors), but soft attention works by taking the expected context vector at that time (i.e. a weighted sum of the annotation vectors using the probability distribution as weights), which is a differentiable action. Hard attention, on the other hand, stochastically chooses a context vector; when the distribution is multinomial over a set of annotation vectors (similar to how soft attention works, but we aren’t calculating the expected context vector now), you just sample from the annotation vectors using the given distribution. The advantage of hard attention is that you can also attend to context spaces that aren’t multinomial (e.g. a Gaussian-distributed context space), which is very helpful when the context space is continuous rather than discrete (soft attention can only work over discrete spaces).

And since hard attention is non-differentiable, models using this method have to be trained using reinforcement learning.

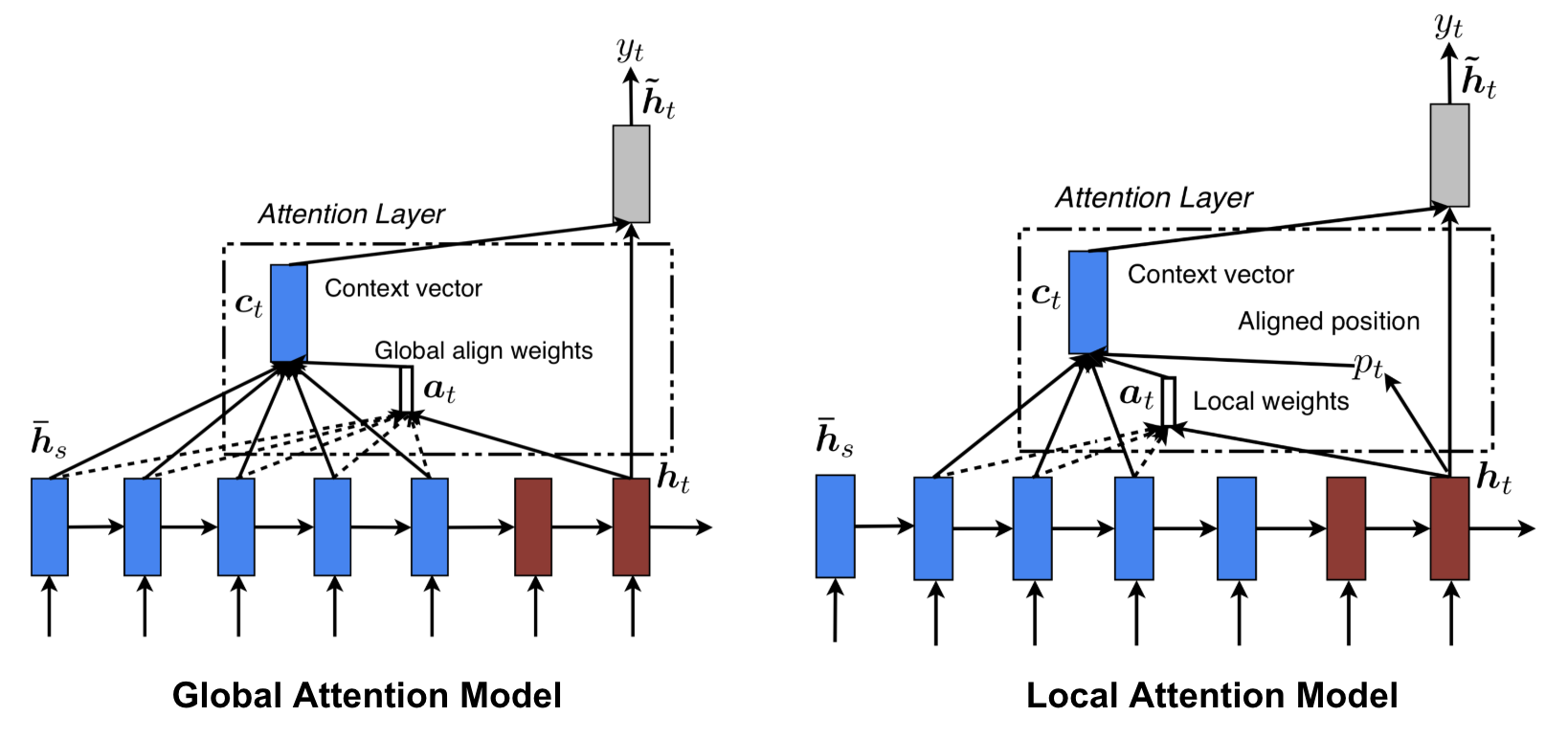
Global and Local Attention

Luong et al. 2015 proposed a global and local attention, where the global attention calculate the entire weighted sum of hidden states for a target output (which is similar to soft attention). While the local attention is more smiliar to the blend of soft and hard attention. For example, in their paper, the model first predict a aligned position for the current target word then a window centred around the source position is used to compute a context vector.

Reference

1. This attention blog heavily borrowed from Lilian Weng’s blog, more details refer to https://lilianweng.github.io/lil-log/2018/06/24/attention-attention.html